理论基础
傅里叶级数:
学过傅里叶级数、傅里叶变换等知识的,都知道,满足[狄利赫里条件]的[周期函数]都能用傅里叶级数来拟合。
狄利赫里条件:
- 在任何周期内,x(t)须绝对可积;在任一有限区间中,x(t)只能取有限个最大值或最小值;
- 在任何有限区间上,x(t)只能有有限个第一类间断点。
傅里叶级数表达式:
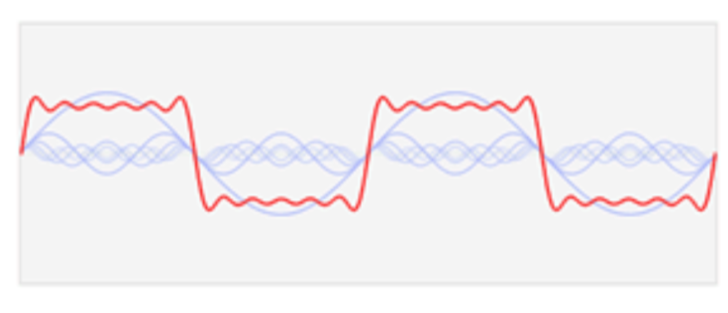
于是,换个思路,是不是也可以用傅里叶级数来绘制各种各样的线条来组合成各种图形呢?答案是肯定的
原理理解
平面点与f(t)的转换
二维图像都是由一些点来构成的,决定点的位置就是(x, y)坐标【以xy平面为例】,因此一个点的坐标可以用一个复数来表示:
而f(t)是可以为复数的,把一系列的点“相加”就可以得到某一时刻的f(t),因此可以将其用傅里叶级数展开。
复数与圆的关系
学过复变函数的同学都知道,一个复数可以进行如下转换:
因此:
复数既可以表示一个点,也可以表示一个向量,因此r可以表示为向量的长度,θ可以表示为向量的角度,当 θ在$ [0, 2\pi]$ 范围内变化时,表示向量在绕原点进行旋转,就构成了一个圆。
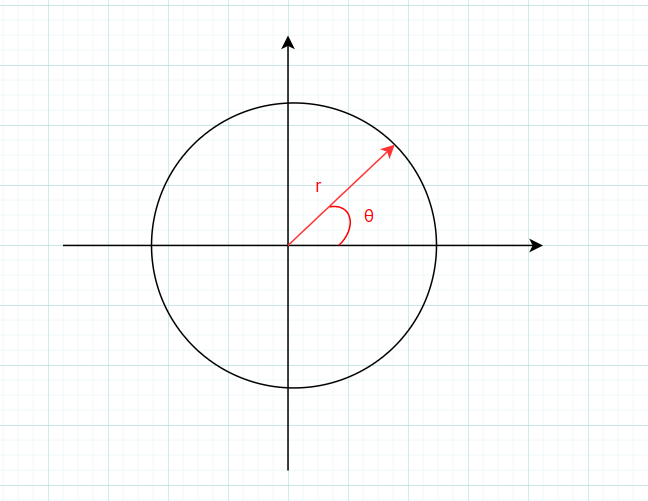
回归正题
重新看这条等式:
f(t)表示我们要绘制的图形在t时刻的一个点,而右边的复指数 ,表示在某一时刻t下,向量长度为 ,角度为 ,ω即向量的旋转速度。
所以右边表示无数个向量的相加,随着时间t不断增加,向量不断旋转,就能不断计算出表示的所有点,把这些点连接就构成了我们要的图形。
注意:需保证一个图形是可以一笔画出来的,即单连通图形,如正方形等;
多个图形可以分别用 等来进行表示,分别进行傅里叶变换。
一个图形的(x, y)坐标是由我们事先确定的,也就是说,我们事先得先确定我们要绘制什么图形,然后把它的轮廓的(x, y)坐标提取出来即可,这个后面再介绍如何通过python提取图像轮廓
确定了(x,y)坐标也就是确定了f(t), 因为f(t)可以是个复数
现在主要是解决如何将展开成傅里叶级数,即确定
-
t是一个时间尺度,随着时间变化而变化,不需要我们去求; -
T为f(t)的周期,由我们绘制的图来决定,即多久绘制完一遍这个图形,通常是这个图(轮廓)的点数。T的单位应该是秒,为什么会是点数呢?其实是用轮廓的所有点N来表示在一个周期的时间内绘制的点数,这样刚好绘制完一遍这个图;
-
j理解成是为了表示这是一个复数,不用管; -
是我们要求的唯一参数,即每个向量的长度值;
在学傅里叶级数时,我们都知道系数 的求法如下:
这是在t为连续条件下的表达式,我们可以将它转为t为离散情况( t 每次变化为):
接下来就是如何通过代码来计算 了
注意k的范围 k表示圆的个数,由自己确定,k越大逼近效果越好,但越大会导致计算复杂度增加,对计算机性能有更高要求,建议最大不超过N(即f(t)的所有点数)
学过数字信号处理的,可以看下DFT的公式
其中 实际就是 ,就是
代码实现
求傅里叶级数的系数
编程语言 Javascript
先实现复数的相加、相乘运算、复指数转为一般指数
在代码中用
z=[a, b]的方式来表示一个复数z=a+jb,其实表示方式无所谓,只要能确定一个复数即可,重要的是要使它能实现复数的一些基本运算
1 | //复数乘法 |
然后求,(代码里用 ”Cn“来表示),写的时候要仔细揣摩公式:
1 | // K=[0, -1,1, -2,2, -3,3 ...] |
求傅里叶级数
然后是根据 求 , 也就是将一个个向量加起来
1 | // cx, cy用于确定在哪里绘制图像,即定位作用 |
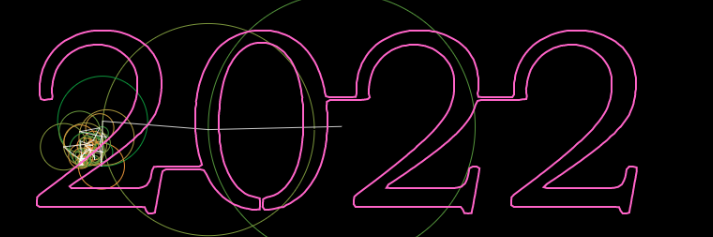
绘制圆和向量:
1 | function DrawCircles(cx, cy, n = 5, imgIndex=0, speed=1) { |
1 |
|
如何通过python提取图像轮廓
上面这些就是绘制图形需要的基本代码,但还有一个重要问题,如何获取图形的轮廓,即获取 【代码中是xn】,只有先得到 才能求出 【代码中的 Cn】
方法一
通过opencv可以轻松获取图像的轮廓,以python3来调用opencv库来提取图片轮廓的方式:
1 | import cv2 |
这是生成的path.txt中的数据

方法二
如果熟悉svg,可以制作成svg矢量图(将自己需要绘制的图通过photoshop等工具描绘出它的轮廓,然后保存为svg图片即可),也可以提取path
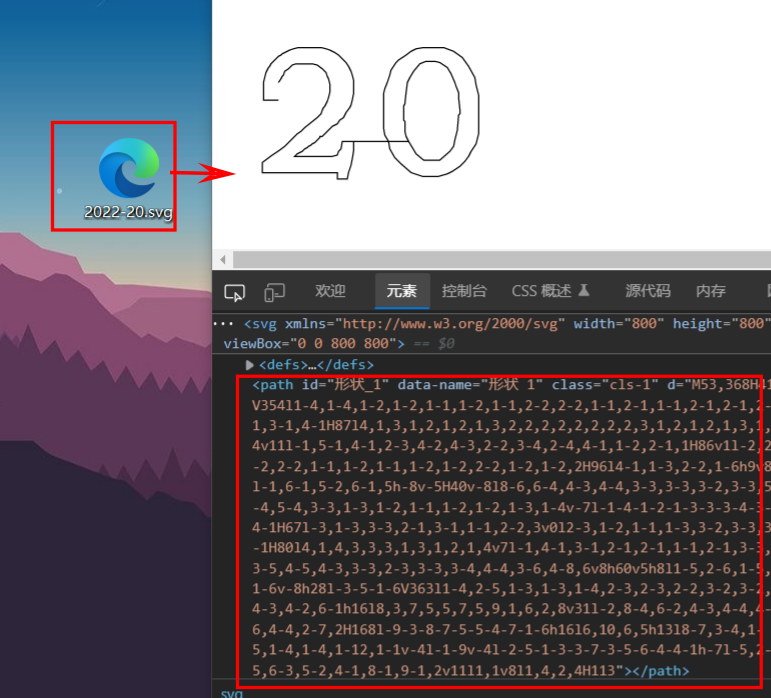
1 | import numpy as np |
两种方式各有优劣,可以根据自己熟悉程度选择
代码用法
完整代码已经放到CSDN托管平台GitCode,码云Gitee平台,需要使用的自行选择前往下载
注:下面获取路径path用的是方法一,方法二跟一差不多
-
首先准备一张图片(图片轮廓可以一笔画出来,最好是黑白且比较明显的),比如:

-
修改
imgProcess/get_path.py图片路径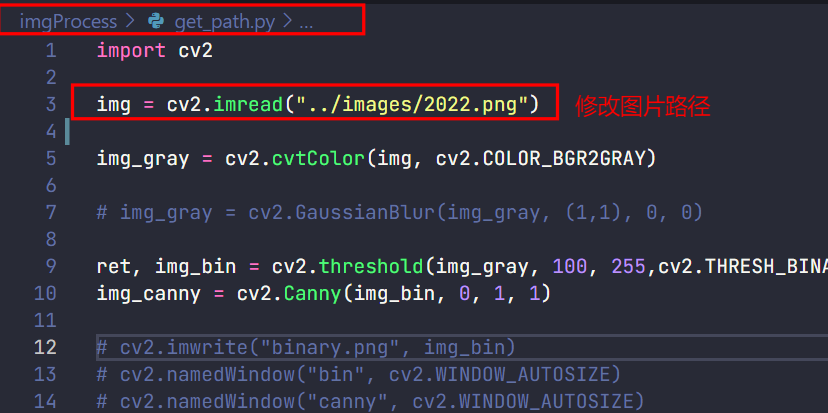
-
打开
imgProcess/path.txt,将数据(会比较多)全部复制到MyFT/js/main.js如下位置
-
初始化
1
2
3
4
5
6//参数依次为:
//第几个pathArr,这里是0
//圆的个数(默认400),这里选择500
//路径存储容量(默认11,内部计算后为2**11),这里不修改
//放大倍数(默认1),这里不放大
initImg(0, 500, 11, 1); -
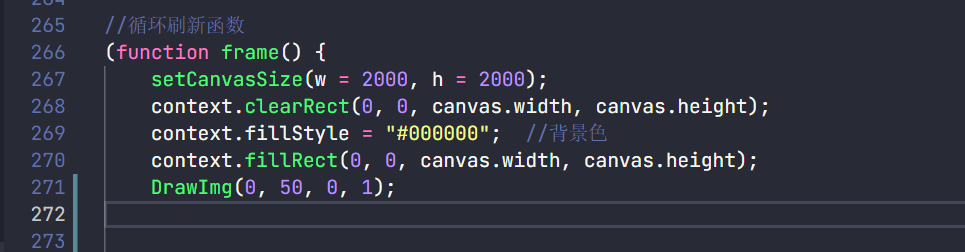
绘图
调用
DrawImg函数,参数依次为 【x坐标(0)、y坐标(50)、第几张图(这里是0)、绘图速度(这里是1)】注:这里的xy坐标只是大概位置
-
修改后打开
MyFT/index.html即可查看效果
参考教程 编码珠玑-手把手教你编写傅里叶动画 (作者写的很好,其公众号编码珠玑含有这一篇文章)


